Contact of Two thin cylinders

Understanding the mechanics of two thin cylinders in contact provides foundational insight into general curved surface interactions encountered in engineering applications. To address the two-body contact having a curved surface, this chapter reviews the contact of two thin cylinders with radii R1 and R2. In this case, it is presumed to be plane stress since the thickness is very small. Because the thickness of the cylinders is negligible compared to their other dimensions, stresses perpendicular to the surface can be considered insignificant, justifying the plane stress assumption.  The top cylinder generates the load ‘W’ along with y-axis. As two bodies deformed, the distance between the two cylinder centers is R1+R2-δ, where δ  is the deformation. Using trigonometry, it can be represented to R1 cosβ1+ R2 cos β2 as illustrated to Fig. 3

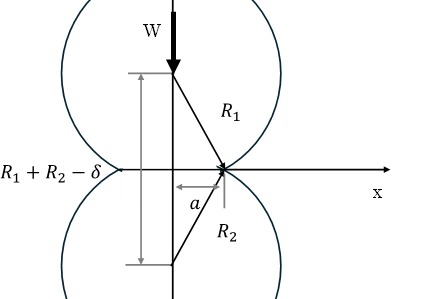
Through Taylor series expression of cosβ, it can be simplified as below:

Using equation (3) , rearrange and simplified shown equation (4). The deformation can be described to the radius of two cylinder as given (5)

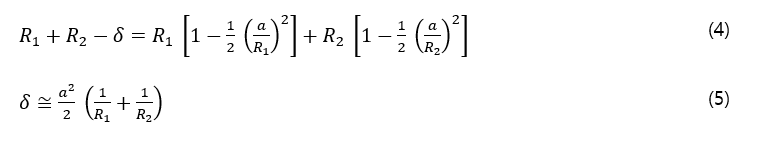
Deformation near the y-axis is considered at two points on each cylinder. As illustrated in Fig. 4, the deformation definition was given.

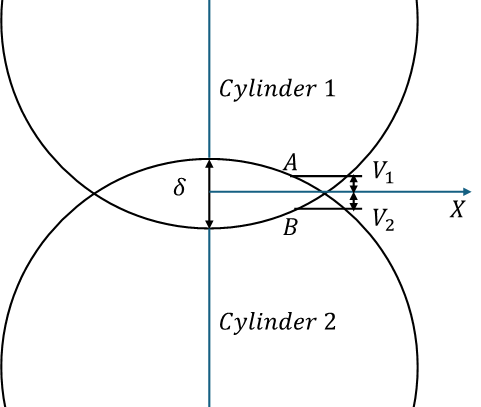
Implement the Hooks law and equation (3) in previous chapter in this deformation derivation for contact width,

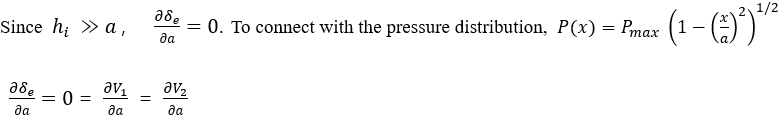
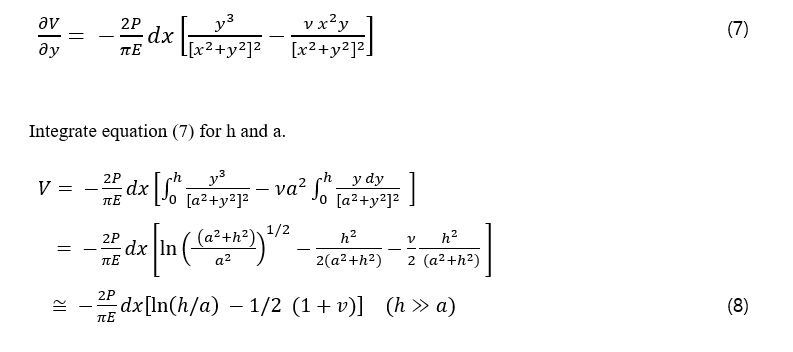
Here, W represents the work done per unit area, and E denotes Young's modulus. This derivation is based on the plane stress condition. To consider plane strain, E should be replaced with E/(1 − ν²), where ν is Poisson's ratio. This substitution ensures that the correct material response is used for the plane strain scenario.