Introduction of Hertzian Contact

In mechanical engineering, materials science, and applied physics, the phenomena that arise when two solid bodies come into contact constitute a central research topic. In particular, the distribution of contact pressure, deformation, and subsurface stress that occurs when bodies with curved surfaces are pressed together is frequently encountered in practical industrial applications such as rolling bearings, gears, and cam–follower systems[1].
One of the most fundamental theoretical frameworks for such contact problems is the Hertzian contact theory. This theory was first proposed in 1882 by the German physicist Heinrich Hertz in his seminal paper “Über die Berührung fester elastischer Körper,” in which he solved the elastic contact problem for ideally smooth, non-adhesive, linear elastic bodies with curved surfaces. Hertz showed that when two elastic solids with curved geometries are pressed together, the nominally point or line contact expands into a finite elliptical (or circular) contact area, and he derived closed-form expressions for the contact area, maximum contact pressure, and three-dimensional stress field as functions of the applied normal load, the radii of curvature, and the elastic properties of the materials[2].
For example, in the case of two spheres in contact, the maximum contact pressure,
{/p_0} , is expressed in terms of the normal load, F, and the contact radius, a, as
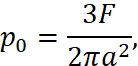
and the maximum shear stress occurs not at the surface but at a certain depth beneath the contact, which provides a rational basis for subsurface-initiated rolling contact fatigue in bearing raceways. Hertzian contact theory is typically formulated for simple geometries such as spheres, cylinders, and planes under frictionless, purely normal loading, yet it supplies essential baseline data for understanding stress concentration, elastic deformation, and fatigue damage initiation in a wide range of rolling and sliding contacts.
In classical mechanics and strength-of-materials–type static analysis, stresses are usually evaluated under the assumption of directly applied loads or bending moments at specific sections of a component. By contrast, in contact problems, the peak stresses often develop beneath the surface due to the highly nonuniform contact pressure distribution, and fatigue cracks can initiate in these subsurface regions under repeated rolling or sliding contact. In rolling bearings, such subsurface rolling contact fatigue has long been recognized as a primary life-limiting mechanism. On this basis, Lundberg and Palmgren proposed in 1947 a probabilistic rolling bearing life theory in which the bearing life is linked to the distribution of orthogonal shear stress within the stressed volume, leading to the well-known L10 life concept and life exponent used in bearing design practice. The theoretical framework of Lundberg–Palmgren [3] was subsequently incorporated and refined in international standards such as ISO 281, which provides standardized methods for calculating the basic and modified rating life of rolling bearings [4].
The present study focuses on understanding the stress distribution in both the contact zone and the subsurface region under Hertzian contact loading and on establishing a finite element method (FEM) modeling procedure for quantitative evaluation of these stresses. FEM allows the Hertzian solution to be extended to more realistic conditions, including complex geometries, material inhomogeneity or anisotropy, and nonlinear contact constraints, thereby enabling more accurate assessment of local stress fields and potential fatigue damage sites in rolling contact components [5,6]